A Diagonal Layout Algorithm for Matrices

This article describes an algorithm for laying out a list of items diagonally in a square, or nearly square, matrix. The algorithm provides a method for compactly arranging sorted items using proximity and has been used to visualize document similarity data. A Java implementation of the algorithm is presented.

1. Introduction

This article describes an algorithm for laying out a list of items diagonally in a matrix. The matrix is either square, or nearly square; the width and height of the matrix differ by at most one. If the values in the list have been sorted, this algorithm provides a method for compactly arranging the items to emphasize the order with proximity. This algorithm has been used to implement a visualization of document similarity data.

2. The Algorithm

I’ll use the following list of 12 items to explain the algorithm:

A B C D E F G H I J K L

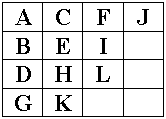
The following examples show these items laid out in square (a) and nearly square matrices (b) and (c). The head of the list is placed in the top left hand corner. The remaining items are arranged diagonally from the top left to the bottom right in the order they occur in the list. If the number of items in the list is larger than the size of the matrix, the extra values are discarded, as illustrated by (a). If the number of items is smaller than the size of the matrix, the remainder of the matrix is left empty (d).

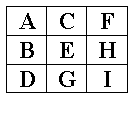
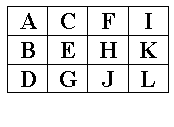
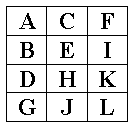
3. Implementation

The following code is a Java implementation of the diagonal layout algorithm. The layout() method has two parameters: an array of values to lay out, items, and a two-dimensional array, matrix, in which the values are to be laid out. To simplify the presentation of the code, the layout() method assumes that the dimensions of matrix are large enough to contain the number of items and does not perform this check.

void layout(char[] items, char[][] matrix) {
    int length = items.length;
    int width = matrix.length;
    int height = matrix[0].length;
    int lastRow = height - 1;

    int a = 0;
    int b = 0;
    int A = 0;
    int B = 0;
    boolean firstColumn = true;

    for (int i = 0; i < length; i++) {
        matrix[a][b] = items[i];
        if (b == height - 1) {
            firstColumn = false;
        }
        b--; a++;
        if (firstColumn) {
            if (b < 0) {
                a = 0; B++; b = B;
            }
        }
        else {
            if ((a == width) || ((a == width - 1) && (b < 0))) {
                A++; a = A; b = height - 1;
            }
        }
    }
}

The local variables a and b of the layout() method represent the next element of the matrix to be filled. The algorithm traverses the elements of the array items and places each element in the array matrix at co-ordinates (a, b). A represents the column that a is reset to after a diagonal has been filled. A is incremented from the first column to the last column. B represents the column that b is reset to after a diagonal has been filled. B is incremented from the first row to the last row while the first column is being filled (firstColumn is true).

The position of the next element is selected by moving up and to the right by decrementing b and incrementing a (figure 6). If the first column is being filled and the row of the next element is above the first row (b < 0), the value of a is reset back to 0 (the first column), the reset row, B, is incremented, and b is set to the new value of B.

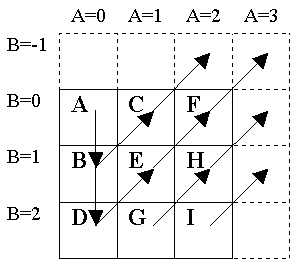
If the columns to the right of the first column are being filled (firstColumn is false) and the value of a, the column of the next matrix element to be filled, extends beyond the most right column of the matrix ((a == width) || …), the value of A is incremented to the right, a is reset to the new value of A, and the value of b is reset to the bottom row of the matrix (height - 1). This process continues until the matrix has been filled.

The following code calculates the dimensions of the smallest square, or nearly square matrix that will hold a specified number of items, size.

int width = (int)(Math.sqrt(size) + 0.5d);
int height = width;
int area = width * height;
if (area < size) {
    width++;
}